Data Compression: Crushing Data Using Entropy

It has been quite some time since our first installment on simple data compression. This second installment is long overdue!

Compression is ubiquitous in our everyday lives. Our OSes handle .zip files natively, we watch high-quality compressed video on our cell phones, we browse the web and see dozens or hundreds of compressed images every day, and even under the hood websites like this one are compressed for faster delivery.

If you are a game developer, you have probably encountered a need to use compression in one form or another. Game engines like Unity and Unreal provide built-in methods of compressing game and texture data as engine features that are transparent to use. In other situations, such as if you have to create networked multiplayer code, you likely would have to spend a lot of time reducing the size of the data you are sending over the network in order to ensure the best possible experience.

Every method of bit-packing has the effect of representing some number of input bits as fewer output bits. In our previous blog on this subject,  we represented 32-bit integers as smaller, variable-length integers. We accomplished this by merely injecting a 5-bit length field and making the first 1-bit of each integer implicit. The result was a reasonably efficient bit-packer. However, the smallest individual symbol a bit packer can use is 1 bit in size. It is possible to store those symbols in fractions of a bit by using an entropy coder like Arithmetic Coding.

Arithmetic coding is very simple. They work by encoding the probability of a symbol into a range on the number line [0...1). Each time a symbol is encoded, it defines an ever-shrinking part of the number line as the next range. The output is a real number of finite length. Here is a simple example:

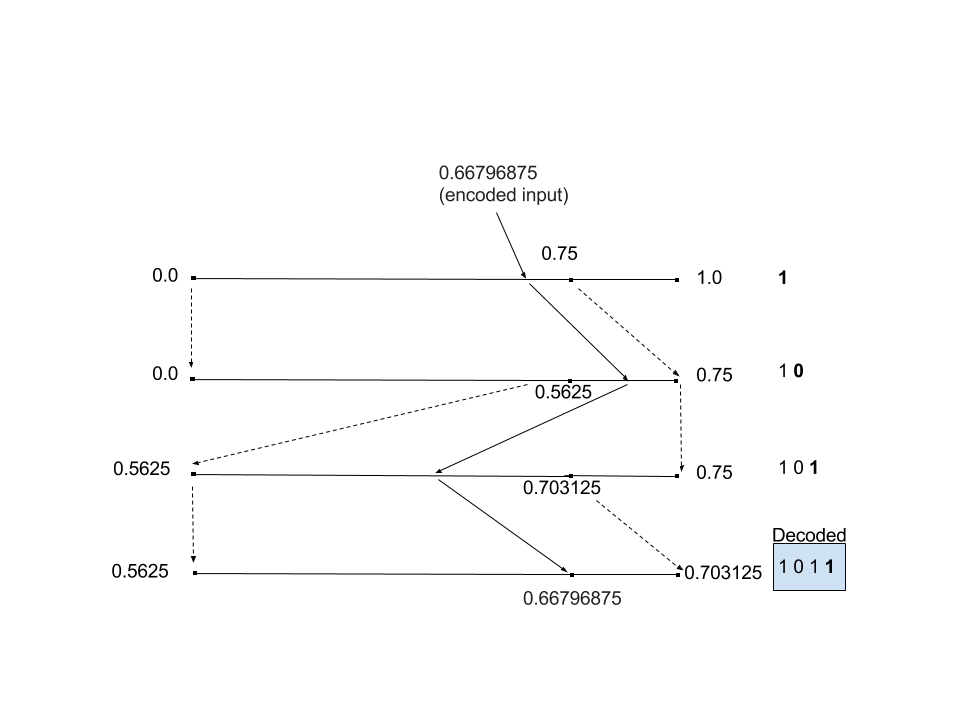
Here is how you encode the first few symbols of a string of bits. At each stage, a symbol gets encoded by tracking the resulting proability. At the first stage, the output is 0.75. We then 'zoom in' on the 0...0.75 range and repeat the process with the probability model. The 0 occupies the upper .25 of the probability space, so we zoom in on the 0.5625...0.75 range. The process repeats until the last symbol is encoded, and the output of the process is 0.66796875.

Here is how the decoding process works:

The decoding process uses the same math to compute the progression of probability ranges. The encoded number will always fall in the correct probability range for the given symbol at each stage, allowing the original data to be decoded. Here we test the encoded message 0.66796875 against each iteration of the probability ranges and emits the symbol associated with the sub-range the value sits in. In this case, 0.6679... sits below 0.75 in the first iteration, so the first symbol is a 1. We then rescale the ranges in the same way as when we encoded and test again. We find that 0.6679... is larger than 0.5625, which sits in the probability range for 0, so we emit a 0. After rescaling the third time, we find that 0.6679... sits below 0.703125, which again puts it in the probability range for 1, and so on. 

What is even more interesting is that at each stage you can change the probability distribution of your symbols, and it still works, and will still decode as long as you switch to the same probability distributions at the same stages as the encoder did.

Now, computers don't store things as arbitrarily-long real numbers, and types like float or double will run out of precision after only a small number of symbols. This is overcome in a very simple way: Just multiply everything by 0x7FFFFFFFh.

You came here for code, so let's get started.

We are using a binary arithmetic coder. There are many implementations out there, such as the one is LibLZMA, however for this blog we are using a port of the coder implemented by Fabian Giesen. His coder is written in C++, however given that most our audience uses C# in Unity, I have ported his encoder and placed in our examples repository, licensed under MIT.

Here is the implementation of the binary arithmetic encoder:

public class BinaryCoder
{
  private UInt32 m_high = ~0u, m_low = 0;
  private Stream m_output;
 
public BinaryCoder(Stream outputStream)
{
  m_output = outputStream;
}

public void Encode(int bit, UInt32 probability)
{
  UInt32 x = m_low + (UInt32)(((UInt64)(m_high - m_low) *
                               probability) >> CoderConstants.PROB_BITS);

  if (bit != 0)
    m_high = x;
  else
    m_low = x + 1;


  // this is renormalization - shift out topmost bits that match
  while ((m_low ^ m_high) < 0x01000000)
  {
    m_output.WriteByte((byte)(m_low >> 24));
    m_low <<= 8;
    m_high = (m_high << 8) | 0x000000ff;
  }
}

public void Flush()
{
  UInt32 roundUp = 0x00ffffffu;
  while (roundUp != 0) 
  {
    if ((m_low | roundUp) != 0xffffffffu)
    {
      UInt32 rounded = (m_low + roundUp) & ~roundUp;
      if (rounded <= m_high)
      {
        m_low = rounded;
        break;
      }
    }

    roundUp >>= 8;
  }

  while (m_low != 0) 
  {
    m_output.WriteByte((byte)(m_low >> 24));
    m_low <<= 8;
  }
  m_output.Flush();
}
}

The binary arithmetic coder looks confusing at first. They have been around for quite some time, and contain various approximations and optimizations, so the math they employ is not immediately familiar. There is a good explanation on how these various optimizations came to be and what they do here.

It is very simple to use, just encode a bit with a probability prediction using the Encode() function. The parameters are the value of the bit, and the probability of the bit being 1. The coder itself is just a way to tracking and emitting encoded bytes, it will not magically make your data smaller until you have a good prediction model. 

Our example code contains a set of models that can be used to attain compression. The simplest one, the SimpleStaticModel, uses a static probability and encodes a given bit using that probability.

Let's look at our example code. We have cooked up some data for the purposes to showing off compression. This is representative of the type of data that is easier to analyze and build a compression scheme for:

byte[] simpleSampleData =
  {
  0x00,
  0x00,
  0x00,
  0x0f,

  0xff,
  0xf0,
  0x00,
  0x1f,

  0xff,
  0xff,
  0xff,
  0xff,

  0xf1,
  0xe0,
  0x0c,
  0xf0
};

An efficient way to encode this is using a run-length (or dgap) scheme to code run-lengths of bits. We encode a series of values to give us the starting state followed by the lengths of the runs, which would encode to {28, 16, 15, 41, 3, 4, 9, 2, 2, 4, 4}, where the first 0 representing the bit starting state, and the remaining bits represting the runs of the alternating states, therefore there are 28 zeros, followed by 16 ones, followed by 19 zeros, etc. This is efficiently encoded using 1 bit for the initial state, and 6 bits for each subsequent value, giving a grand total of 67 bits ~ about 8.375 bytes! 8.375 bytes/16 bytes = a compressed size of 52%! However, it will encode to 9 bytes because everything must be, at a minimum, byte-aligned. You will also need two other pieces of information: The initial bit state, and the number of encoded dgaps, which in this case can all be done using a 5-bit header, bringing the total output size to 9 bytes.

That's pretty efficient. Now Let's see what happens when we use a simple binary coder fed by a simple adaptive probability model.
 

{
  System.IO.MemoryStream output = new System.IO.MemoryStream();
  BinaryCoder coder = new BinaryCoder((Stream)output);
  BinShiftModel adaptiveModel = new BinShiftModel();

  // the lower the number, the faster it adapts
  adaptiveModel.Inertia = 1;

  foreach (byte b in simpleSampleData)
  {
    for (int bitpos = 7; bitpos >= 0; --bitpos)
    {
      int bit = (int)(b >> bitpos) & 1;
      // NB: Skipping try/catch here!
      adaptiveModel.Encode(coder, bit);
    }
  }
  coder.Flush();

  Console.WriteLine("Adaptive Output size is " + output.Length);
}

The result reduces the data by just a few bytes. Not nearly as good as our tailored bit-packing result. This an important lesson: Using entropy alone for packing bits is NOT a silver bullet. In fact, with real-world data, entropy is probably going to  make your data bigger. Why? Entropy works based on accurate predictions. Guess correctly, you get a little benefit. Get it wrong by the same amount, get punished much more.

The number of bits required to encode a given symbol can be calculated using -log2(Psym). Let's lay you figure you have a 70% chance of encoding a 1 bit, but when you read the next bit you want to encode it comes up a 0. That bit is going to encode to 1.74 (-log2(1-.70)) bits in the output stream - you lost almost 1 whole bit! Had you been lucky and actually read a 1 bit instead, you would have encoded it with 0.51 bits (-log2(.70)), you would have saved .49 bits of space, whereas the mis-prediction costs you an additional .74 bits.

Think of it this way, the better you can predict the future, the better entropy works.

Let's try another way to compress our data. This time, rather than be adaptive, we'll come up with some fixed probabilities that work well. We can compute this ahead of time. For the above dataset, we have 128 bits. 10 of these bits 'transition', that is, they are the last of a series of 1 or 0, and the proceeding bit will be in the opposite state. The means that the probability of the next bit being the same state as the current bit is about 92%.

The implementation works as such: We encode 0 bits with a 8% probability of being 1, and we encode 1 bits with 92% probability of being one. We can implement this using two static models: One of the models is used when encoding runs of 0's. This model has a low probability of 1 because while you're encoding 0's there is little chance that they will encounter a 1. The other model is the opposite, it encodes with a high probability of 1 because you are unlikely to encounter a zero. 

Another important step is that you encode the current bit with the last model you used, regardless of the bit's value. So if you are encoding 0's, and then you suddenly encounter a 1, you will encode the 1 with the same model as the previous 0's, then you will switch to the 1-biased model. The reason for this is that when decoding, you won't know ahead of time what the next decoded symbol will be, and you need to follow the same rules. This switching of models during encoding/decoding is called a "context switch". What is very interesting here is that, as long as you preserve the encoder state, you can dynamically switch out the probability models as you go. The only requirement is that whatever you do during encoding, you are able to duplicate during decoding. 

For this example, we are going to set aside our adaptive probability model for now and just use the simpler static probability model with context switching:

{
  // encode
  System.IO.MemoryStream output2 = new System.IO.MemoryStream();
  BinaryCoder coder2 = new BinaryCoder((Stream)output2);
  SimpleStaticModel model0 = new SimpleStaticModel();
  SimpleStaticModel model1 = new SimpleStaticModel();

  model0.SetProb(10f / 128f);
  model1.SetProb(1f - (10f / 128f));

  bool use0Context = true; // 0 bits come first, use the correct model!

  foreach (byte b in simpleSampleData)
  {
    for (int bitpos = 7; bitpos >= 0; --bitpos)
    {


      int bit = (int)(b >> bitpos) & 1;

      // encode using the correct context
      // NB: Skipping try/catch here!
      if (use0Context)
        model0.Encode(coder2, bit);
      else
        model1.Encode(coder2, bit);

      // switch context AFTER the bit state changes
      use0Context = (bit == 0 ? true : false);
    }
  }
  coder2.Flush();

  Console.WriteLine("Ideal static model with context switch size is " 
                    + output2.Length);

  /* The decoder looks much like the encoder. 
  Notice how the context switch occurs only
  after a symbol is decoded, exactly as the encoder does it.
  */

  output2.Seek(0, SeekOrigin.Begin);


  // decode
  BinaryDecoder decoder2 = new BinaryDecoder((Stream)output2);
  SimpleStaticModel staticModel0dec = new SimpleStaticModel();
  SimpleStaticModel staticModel1dec = new SimpleStaticModel();

  staticModel0dec.SetProb(10f/128f);
  staticModel1dec.SetProb(1f - (10f/128f));

  bool use0ContextDec = true; // 0 bits come first, use the correct model!
  foreach (byte b in simpleSampleData)
  {
    for (int bitpos = 7; bitpos >= 0; --bitpos)
    {

      int bit = (int)(b >> bitpos) & 1;

      int decBit;

      // decode using the correct context!
      // NB: Skipping try/catch here!
      if (use0ContextDec)
        decBit = staticModel0dec.Decode(decoder2);
      else
        decBit = staticModel1dec.Decode(decoder2);

      /* the decoded bit should match the source bit for the 
      decoder to have worked*/
      if (decBit != bit)
      {
        Console.WriteLine("Error, static example 1 did not decode properly!");
      }

      // switch context when the bit state changes
      use0ContextDec = (decBit == 0 ? true : false);
    }
  }
}

And just like that, it encodes to 6 bytes. In theory, it should encode to 6.3 bytes, however binary range coders aren't 100% efficient, mostly because they have to flush extra bits to renormalize. For this (obviously) cooked data set, this is probably the most ideal representation of its compressibility in it's raw form.

One last note: Entropy coding with an arithmetic encoder is time consuming, though it is actually fast enough for many applications, especially if you can reduce the amount of input data bits you have to encode beforehand. Encoders like gzip can also be useful in many situations, as they perform well and are general-purpose. However, a specific-purpose entropy coder will beat out a general-purpose one, all else being equal, in both CPU performance and compression ratio.

I hope you enjoyed this follow-up installment. Time permitting, I may follow up with another in the future with a more complicated application of entropy encoding. Until then, I hope you have learned enough in this post to be able to dig into some of the common general-purpose compressors out there.

Happy coding!